Search Engine Ranking Models – Ultimate Guide

In recent years, with the rapid growth of the World Wide Web and the difficulty in finding the information you want, efficient and effective information retrieval systems have become more important than ever, and the search engine has become a major tool for many people. The ranking system, a central component in every search engine, is responsible for matching the processed queries and indexed documents.

Due to its central role, much attention has been paid and continues to be given to the research and development of ranking technologies. In addition, ranking is also essential for many other information retrieval applications, such as filtering, answering questions, multimedia retrieval, text aggregation, and online advertising. The use of machine learning technologies in the ranking process has led to innovative and other effective ranking models, and has led to the emergence of a new research area of ​​the name – ranking training or Learn-to-Rank.

Before proceeding with the examination of the models, it is important to emphasize that there are no uniform ranking models and that each model or group of models is used according to the relevant problem that needs to be solved. There are many different scenarios and ranking models that are of interest for document retrieval. For example, sometimes we need to rank documents purely according to their relevance to the request. In other cases, we need to look at the links of similarity, the structure of websites and the variety of documents in the ranking process. This is also called relational ranking.

Conventional ranking models

Many ranking models have been proposed in the information retrieval literature. They can be roughly categorized as relevance and relevance ranking models.

Models for relevancy ranking

The purpose of the relevancy ranking model is to draw up a list of classified documents according to the relevance between those documents and the search query. Although not necessary, for ease of implementation, the relevance ranking model typically takes each individual document as input and calculates a result that measures the correspondence between the document and the request. Then all the documents are sorted in descending order according to their results.

Early relevance ranking models retrieved documents based on the appearance of concepts / words from a search query. Examples include the Boolean model. In principle, these models can predict whether a document is relevant to the request or not, but they cannot predict the degree of relevance.

The Vector Space (VSM) model is proposed to further model the degree of relevance. Both documents and inquiries are presented as vectors in Euclid space in which the internal calculation of two vectors can be used to measure their similarities. To obtain effective vector representation of the application and documents, the TF-IDF calculation is widely used.

Popular models:

• BM25
• VSM
• LSI- Latent Semantic Indexing
• Language Model For Information Retrieval – LMIR

Importance ranking models

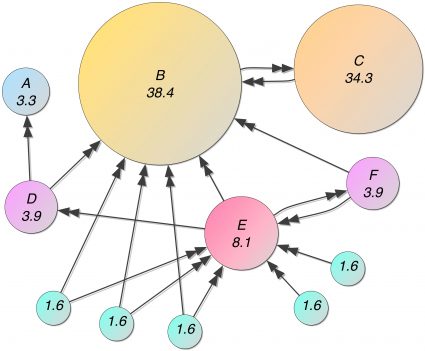
One of the most popular models here is the so-called PageRank model. PageRank uses as a basic criterion the likelihood of a user arbitrarily clicking links to be taken to a particular web page to account for the likelihood of a link being weighted. Many algorithms have been developed to further improve PageRank’s accuracy and efficiency. Some focus on speeding up calculations, while others focus on refining and enriching the model. Examples are topical-sensitive PageRank and Query-dependent PageRank. It is assumed that links from pages with the same theme will weigh more than links with other topics.

Algorithms are also offered that can generate a stable ranking of importance over spamming links. For example, TrustRank is an importance ranking algorithm that considers the reliability of web pages when calculating the importance of pages. In TrustRank, a set of trusted pages are first identified as home pages. Then the trust on the homepage spreads to other pages in the web link graph. Because TrustRank distribution starts from trusted pages, TrustRank can be more spam-resistant than PageRank.

Estimates based on request-level positions

Given the large number of ranking models, a standard rating mechanism is needed to select the most effective model. Indeed, evaluation has played a very important role in the history of information retrieval. Information retrieval is an empirical science and it is a leader in computer science for understanding the importance of relevance and comparative analysis. Information retrieval is well served by the Cranfield Experimentation methodology, which is based on joint collections of documents, information needs (inquiries) and relevance assessments.

By applying the Cranfield paradigm to document retrieval, the relevant evaluation process can be described as follows:

• Collect a large number of (randomly extracted) queries to form a test set.
• For each request q- Collect the documents {dj} m j = 1 associated with the request.
• Take the judgment on the appropriateness of each document through a human evaluation.
• Use a ranking model to rank the documents.
• Measure the difference between the results of the ranking and the assessment of appropriateness using an evaluation measure.
• Use the average measure for all queries in the test set to evaluate the performance of the ranking model.

A number of strategies can be used for the collection of request documents. For example, a person can simply collect all the documents containing the requested word. One may also choose to use some predefined ranking systems to obtain documents that are more likely to be relevant.

A popular strategy is the merger method used in TREC. This method creates a pool of potentially relevant documents by sampling documents selected from the various participating systems. In particular, the top 100 documents received in each submission cycle for an application are selected and consolidated into the human evaluation space.

Learn-to-Rank & Machine Learning

The previous section introduced many ranking models, most of which contain parameters. For example, in BM25 there are parameters k1 and b, parameter λ in LMIR and parameter α in PageRank. In order to achieve a relatively good ranking (in terms of evaluation measures), these parameters must be set using a validation set. Nevertheless, parameter tuning is far from trivial, especially given that the assessment measures are discontinuous and indifferent in terms of parameters.

In addition, a model perfectly tuned to the training set sometimes performs poorly on unseen test requests. This is usually called over-fitting. Another question is about the combination of ranking models. Given that there are many models in the literature, it is natural to explore how to combine these models and create an even more effective new model. However, this combination and its effectiveness are still in question.

While information retrieval researchers have described and sought to address these issues, machine learning has proven to be effective in automatically adjusting parameters, combining multiple features, and avoiding over-adaptation. Therefore, it seems quite promising to adopt machine learning technologies to solve the aforementioned ranking problems.

However, most of the most up-to-date ranking training algorithms are learning the optimal way to combine the required query and document pairing features with discriminatory training. Ranking methods have the following two properties, which can be divided into 2 types:

Featured based

A feature-based feature means that all documents under study are represented by feature vectors that reflect the compliance of the documents with the search query. That is, for an application q, the related document d can be represented by a vector x = Φ (d, q), where Φ is a function extractor. Typical features used in ranking training include the frequency of terms requested in the document, the output of the BM25 model and the PageRank model, and even the relationship between a document and other documents. These features can be extracted from the search engine index.

Even if the function is the output of an existing extraction model, in the context of ranking training it is assumed that the parameter in the model is fixed and the training is carried out in the optimal way to combine these characteristics. In this sense, automatic parameter tuning of existing models before has not been categorized as “training for ranking” methods.

The ability to combine many features is an advantage of ranking training methods. It is easy to incorporate any new advances in model extraction by incorporating model output as one dimension of characteristics. This is true for popular search engines as it is almost impossible to use just a few factors to meet the complex information needs of web users.

Discriminative Training

Discriminatory training “Discriminatory training” means that the learning process can be well described by the four components of discriminatory training – input, output, hypothesis, training set with loss function. That is, the classification learning method has its own input space, output space, hypothesis space, and loss function.

In machine learning literature, discriminatory methods are widely used to combine different types of characteristics without the need to define a probability framework to represent object generation and predictive accuracy.

Discriminatory learning is an automatic learning process based on learning data. This is also one of the requirements for popular search engines for implementation, because every day this search engines will receive a lot of user feedback and data.

Learn-to-Rank Framework

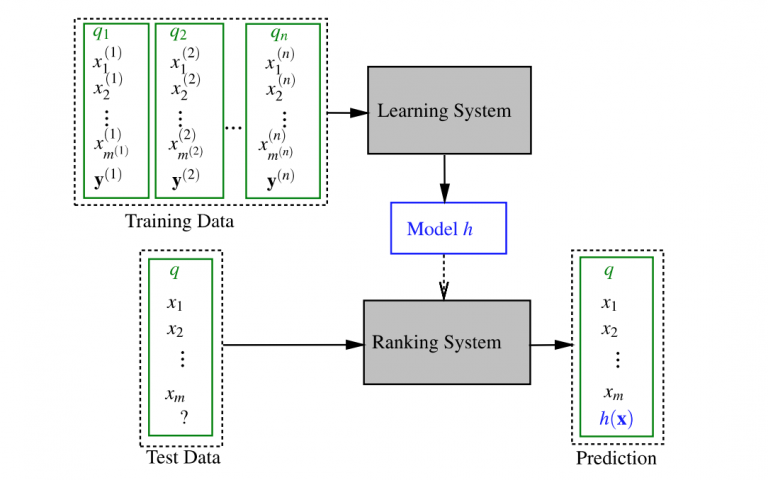
From the figure we can see that when training for classification, as a type of controlled training, a set of trainings is required. A typical training set consists of n training queries qi (i = 1,…, n), their related documents represented by function vectors x (i) = {x (i) j} m (i) j = 1 ( where m (i) is the number of documents related to application qi) and the relevant judgments of relevance. Then, a specific learning algorithm is used to learn the ranking model (i.e., how the characteristics are combined) so that the output of the ranking model can predict the etiquette of the underlying truth in the training set as accurately as possible with respect to loss function. In the test phase, when a new request appears, the model learned in the training phase is applied to sort the documents and return the relevant ranked list to the user in response to his / her request.

Basic approaches to ranking training

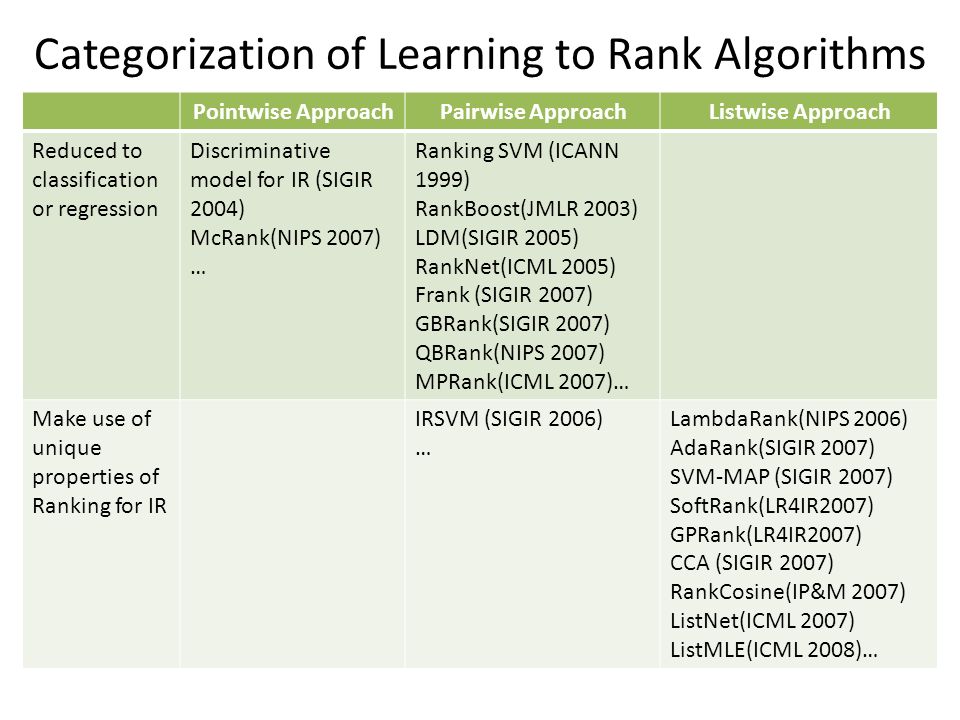
Pointwise Ranking

When we use machine learning technologies to solve the ranking problem, probably the simplest way is to check that existing training methods can be applied directly. In doing so, one assumes that the exact degree of relevancy of each document is what the models will predict, although this may not be necessary since the goal is to achieve a ranked list of documents. According to the different machine learning technologies used, the pointwise approach can be further subdivided into three subcategories: regression-based algorithms, classification-based algorithms, and ordinal regression-based algorithms.

For regression-based algorithms, the output space contains real-valued results; for classification algorithms, the output space contains unordered categories; and for algorithms based on ordinal regression, the output space contains ordered categories.

Point approaches consider one document at a time in the loss function. They essentially take one document and train a classifier / regressor on it to predict how appropriate it is for the current application. Final ranking is achieved by simply sorting the list of results on these documents. For point approaches, the score for each document is independent of the other documents that are on the results list for the request. All standard regression and classification algorithms can be directly used for pointwise ranking training.

The entry space of the point approach contains a vector of each document element. The output space contains the degree of compliance – relevance of each document. The different types of judgment can be made into the main labels of truth in terms of relevance as a degree:

• If the decision is given directly as a degree of relevance lj, the basic truth label for the document xj is defined as yj = lj.
• If judgment is given as a double preference – pairwise lu, v, one can obtain ethics as a basic truth by counting the frequency of a document over other documents.
• If the estimate is given as the general order πl, the basic truth label can be obtained by using a mapping function. For example, the position of a document in πl can be used as a basic truth.

Kinds:

• Regression-based models
• Models based on classification
• Models based on ordinal regression

Pairwise ranking

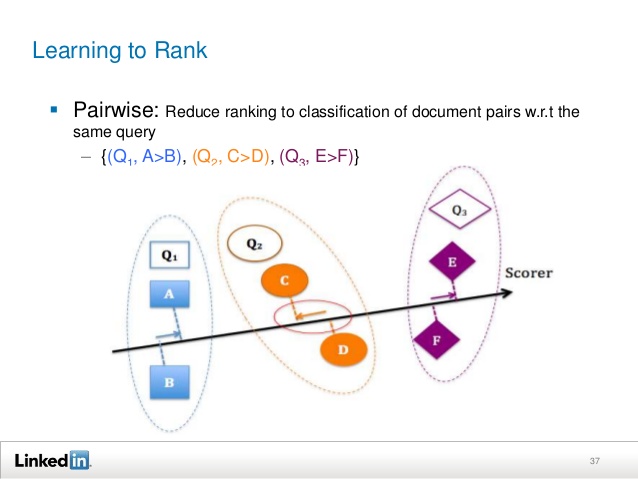
The doubles approach does not focus on accurately predicting the relevance of each document, but instead takes care of the relative order between the two documents. In this sense, it is closer to the concept of ‘ranking’ than the pointwise approach. In the dual approach, ranking usually comes down to the classification of pairs of documents, ie. to determine which document in a pair is preferred. That is, the purpose of the training is to minimize the number of missing classified pairs of documents. As a last resort, if all pairs of documents are correctly classified, all documents will be classified correctly. Note that this classification differs from the pointwise approach classification in that it operates on every two documents under study.

It is a natural concern that pairs of documents are not independent, which violates the basic assumption of classification. The fact is that, although in some cases this assumption is not really true, classification technology can still be used to teach a ranking model. However, another theoretical framework is needed to analyze the aggregate data of the model’s learning process.

Models:

• SortNet
• RankNet
• FRank
• Rank Boost
• Models based on preference
• Ranking SVM
• GBRank
• Multiple Hyperplane Ranker
• Magnitude-Preserving Ranking
• IR-SVM
• Robust Pairwise Ranking with Sigmoid Functions
• P-norm Push
• Ordered Weighted Average for Ranking
• LambdaRank
• Robust Sparse Ranker
• LambdaMart

Listwise Ranking

Listwise’s approaches directly look at the entire list of documents and try to build their optimal ordering. There are 2 basic sub-techniques for listing:

Ranking teaching: Direct optimization of IR metrics such as NDCG. For example SoftRank, AdaRank.
Minimize the loss function that is determined by understanding the unique properties of the type of ranking you are trying to achieve. For example, ListNet, ListMLE. Listed approaches can be quite complex compared to pairwise or pointwise approaches.
The entry space of the list approach contains a set of documents related to query q, for example, x = {xj} m j = 1. The exit space of the list approach contains the list with ranking (or permutation) of documents. Different types of judgments can be made into basic truth labels for a ranked list:

If judgment is given as a degree of relevance lj, then all permutations that are consistent with judgment are major true permutations. Here we define permutation πy as corresponding to the degree of relevance lj, if ∀u, v satisfying lu> lv, we always have πy (u) <πy (v). In this case, there may be many basic truths. We use Ωy to represent the set of all such permutations.

If judgment is given as a double preference, then again all permutations that are consistent with the dual preferences are permutations of the basic truth. Here, we define permutation πy as consistent with the preferences lu, v, if ,u, v satisfying lu, v = +1, we always have πy (u) <πy (v).
Again, there can be many basic true permutations in this case, and we use Ωy to represent the set of all such permutations.

Such treatment can be found in the definition of rank correlation:

If the estimate is given as the general order πl, it can be directly determined πy = πl. Note that in the list approach, the output space that facilitates the learning process is exactly the same as the task output space. In this regard, the theoretical analysis of the list approach may have more direct value in understanding the real ranking problem than the other approaches when there are discrepancies between the facilitating learning space and the real task output space. The hypothesis space contains multivariable functions h that work on a set of
documents and predict their permutation.

For practical reasons, the hypothesis h is usually realized with an evaluation function f, for example h (x) = sorting ◦ f (x). That is, the evaluation function f is first used to evaluate each document, and then these documents are sorted in descending order of results to obtain the desired permutation.

There are two types of loss functions widely used in the listwise approach. For the first type, the loss function is explicitly related to the valuation measures (which we call the loss-specific loss function), while for the second type the loss function is not related. Note that it is sometimes not very easy to determine whether the loss function is sequential, as some list loss line items can also be considered pointwise or pairwise.

In this article, we mainly distinguish loss by point or double loss according to the following criteria:

• The list loss function is defined with respect to all documents related to a request
• The list-losing function cannot be completely decomposed to a simple summation on single documents or pairs of documents
• The List Loss function emphasizes the concept of a ranked list and document positions in the end result are visible.

Types and models:

Minimization of Measure-Specific Loss

• Measure Approximation
• Bound Optimization
• Non-smooth Optimization

Non-measure-Specific Loss Minimization

• ListNet
• ListMLE
• Ranking Using Cumulative Distribution Networks
• BoltzRank